深度度量学习

距离度量学习

在搜索任务中，给定查询样本和候选集合，我们一般采用的步骤是：1）提取样本特征；2）计算查询与候选样本特征之间的距离；3）返回距离最小的候选作为搜索结果。

常用的度量样本之间距离的方法包括欧式距离，余弦距离，汉明距离等。然而单一的距离度量方式难以适用不同场景下的搜索任务，已有的距离方式本身也可能存在缺陷，如欧式距离假设特征所有维度的权重相同，因此如何从数据中学习出有效的距离度量成为许多研究者关注的问题。

距离度量学习（Distance Metric Learning）算法一般是学习一个马氏矩阵，从而两个样本点 $\boldsymbol{x}_{i}$ 和 $\boldsymbol{x}_{j}$ 之间的距离定义为

$$D_{\boldsymbol{M}}(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = (\boldsymbol{x}_{i}-\boldsymbol{x}_{j})^\top \boldsymbol{M} (\boldsymbol{x}_{i}-\boldsymbol{x}_{j})$$

距离度量学习在人脸验证和行人再识别场景中研究较多，如 Margin Nearest Neighbor Learning (LMNN)，Information Theoretic Metric Learning (ITML) ，Logistic Discriminant Metric Learning (LDML) ，KISSME， XQDA，Probabilistic Relative Distance Comparison (PRDC) 等。

基于距离度量矩阵学习的方法虽然多种多样，本质均是基于匹配样本距离小于非匹配样本距离的假设来定义不同的目标函数和约束条件，且求解方法多种多样。该方法在搜索阶段中一般利用学习到的马氏矩阵快速计算特征间的距离，效率较高。

深度度量学习

随着深度学习的兴起，研究者们开始关注如何利用深度神经网络学习好的样本特征，从而在特征映射空间中采用简单的欧式或余弦距离即可正确度量样本之间的距离，我们将其称为 深度度量学习（Deep Metric Learning）。

经典损失函数

深度度量学习的研究重点在于如何定义一个好的损失函数，来指导网络学习到具有判别能力的特征。经典的度量学习损失函数包括对比损失函数（Contrastive Loss）和三元组损失函数（Triplet Loss）。

Contrastive Loss

对比损失函数（Contrastive Loss）起源于 Yann LeCun 等人在CVPR 2006上提出的 Dimensionality Reduction by Learning an Invariant Mapping (DrLIM) 算法，其主要思想是在学习降维映射函数时，相似的输入要被映射到低维空间相近的点，而不相似的输入则要被映射到相距较远的点。

给定两个输入样本 $X_{i}$ 和 $X_{j}$ ，以及匹配标签 $y_{i,j} \in \{0, 1\}$，其中 $y_{i,j}=1$ 表示两个样本相似，$y_{i,j}=0$ 表示不相似，降维映射函数 $G_{\boldsymbol{W}}$，对比损失函数定义为

$$L_{contrast}=y_{i,j} \frac{1}{2} D_{i,j}^2 + (1 - y_{i,j}) \frac{1}{2} [m - D_{i,j}^2]_+$$ 其中 $D_{i,j}=\|G_{\boldsymbol{W}}(X_{i}) - G_{\boldsymbol{W}}(X_{j})\|_{2}$ 为映射向量之间的欧式距离，hinge 函数 $[z]_+=\max(z,0)$，$m$ 为阈值参数。该公式表明我们希望相似样本之间的距离尽可能小，而不相似样本之间的距离要大于阈值m。

Triplet Loss

三元组损失函数（Triplet Loss）由 Florian Schroff 等人在 CVPR 2016上提出，其主要思想是最小化目标样本与正样本之间的距离，同时最大化目标样本与负样本之间的距离。

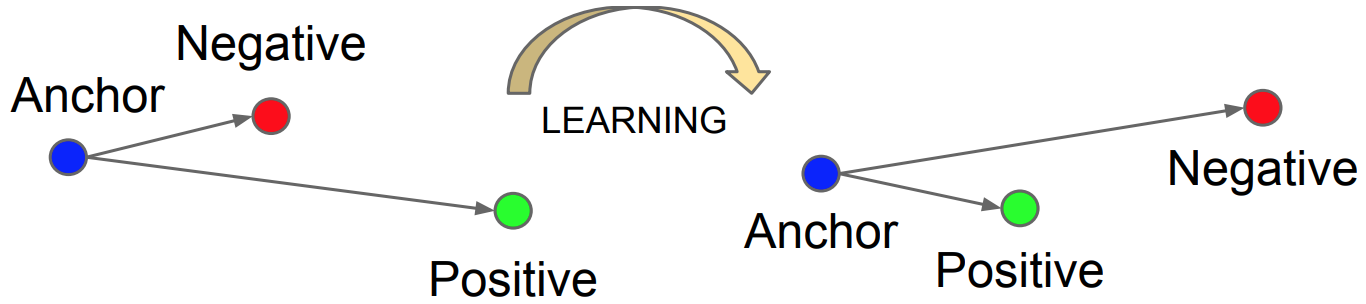
triplet

给定目标样本 $\boldsymbol{x}_{i}^{a}$ ，正样本 $\boldsymbol{x}_{i}^{p}$ 和负样本 $\boldsymbol{x}_{i}^{n}$ ，以及网络 $f$，三元组损失函数定义为

$$L_{tri}= [\|f(\boldsymbol{x}_{i}^{a}) - f(\boldsymbol{x}_{i}^{p})\|_{2}^{2} - \|f(\boldsymbol{x}_{i}^{a}) - f(\boldsymbol{x}_{i}^{n})\|_2^{2} + m, 0]_{+} $$ 其中 $m$ 为阈值参数，作者在计算样本间欧式距离前对特征进行了归一化，即 $\|f(\boldsymbol{x})\|_{2}=1$。该公式表明我们希望正样本对与负样本对之间的距离间隔至少为$m$ 。

从实际经验来看，Triplet Loss 在很多情况下表现会比 Contrastive Loss 好一些，目前也已广泛应用于各种涉及到度量学习的任务中。Quora 上讨论了一些可能的原因：

Triplet Loss is less “greedy”，Contrastive Loss 要求相似样本间的距离越小越好，但 Triplet Loss 仅要求样本对距离之间的间隔满足阈值范围；

距离本质上是个相对概念，当我们认为 $\boldsymbol{x}_{i}^{a}$ 与 $\boldsymbol{x}_{i}^{p}$ 之间相距较近时，是因为相比之下 $\boldsymbol{x}{i}^{a}$与$\boldsymbol{x}{i}^{n}$之间相距更远；而当我们把 $\boldsymbol{x}_{i}^{n}$ 移动得与 $\boldsymbol{x}{i}^{a}$更近时，那我们就不再认为$\boldsymbol{x}{i}^{a}$与 $\boldsymbol{x}_{i}^{p}$ 相距很近了；Triplet Loss 是从相对距离上进行约束，而 Contrastive Loss 只考虑两个样本点之间的绝对距离。

— What are the advantage of using triplet loss function over a contrastive loss? How would you decide which to use?

笔者个人更倾向于第一种解释，尽管我们希望相似样本距离近，不相似样本距离远，但 Contrastive Loss 并不对相似样本的距离进行限制，网络在学习过程中会不断最小化相似样本距离，这样容易导致过拟合，或掉入较差的极小点。尽管距离远近是相对的，但我们计算的（归一化）欧式或余弦距离会有个范围（如［0，2］之间），绝对距离还是可以提供远近信息，如我们还是认为1.3距离较远，0.1距离较近。也有研究者将绝对距离和相对距离进行综合考虑来进一步提升算法性能。

Triplet Loss 虽然在很多应用中表现出不错的性能，但其也存在着两大问题：1）如何选择三元组？2）如何设定阈值？ Schroff 等人指出我们并不需要离线枚举所有的三元组，因为大部分三元组满足约束条件，对训练网络并没有贡献，还会降低收敛速度。然而，针对每个标记的 anchor-positive pair 选择最难负样本（hardest negative）也很容易导致网络掉入较差的极小点，因此他们提出了一种 online semi-hard negative sampling 策略，即在每个mini batch 中选择到 anchor 距离大于正样本但并没有超过相对距离阈值的负样本。为了选择有效的三元组，他们在实验中设置了较大的 batch size：

The main constraint with regards to the batch size, however, is the way we select hard relevant triplets from within the mini-batches. In most experiments we use a batch size of around 1,800 exemplars.

— FaceNet: A Unified Embedding for Face Recognition and Clustering

针对阈值选择，该文并没有进行比较深入的讨论，一般根据经验设置 $m=0.2$。

研究者们在不同的应用场景中对 Triplet Loss 进行了一系列改进，Chen 等人在 CVPR2017 上针对行人再识别提出四元组损失函数 Quadruplet Loss，定义如下：

$$L_{quad}= \sum \limits_{i,j,k} [g(\boldsymbol{x}_{i}, \boldsymbol{x}_{j})^2 - g(\boldsymbol{x}_{i}, \boldsymbol{x}_{k})^2 + \alpha_1]_{+} + \sum \limits_{i,j,k,l}[g(\boldsymbol{x}_{i}, \boldsymbol{x}_{j})^2 - g(\boldsymbol{x}_{l}, \boldsymbol{x}_{k})^2 + \alpha_1]_{+} $$ $$s.t. s_i = s_j, s_i \neq s_k, s_i \neq s_l, s_l \neq s_k$$

Quadruplet loss 在 triplet loss（第一项）基础上增加了不同类别负样本之间的距离约束（第二项），从而进一步增大学习到特征的类间差异。

Wang 等人在ICCV2017上提出 Angular Loss，约束三元组样本构成三角形中以 $x_n$ 为顶点的的夹角越小越好，其形式如下：

$$L_{ang}=\left[\|\boldsymbol{x}_a - \boldsymbol{x}_p\|^2 - 4\tan^2\alpha\|\boldsymbol{x}_n-\boldsymbol{x}_c\|^2 \right]_+$$

其中 $\alpha$ 是角度超参，一般取 $36^{\circ} \leq \alpha \leq 55^{\circ}$。有意思的是，该文从求梯度角度阐述 Angular Loss 的优越性，Triplet Loss 在求梯度时仅依赖两个样本点，而 Angular Loss 则同时考虑了参与损失函数计算的三个样本点。

$~~~~~~~~~~~~~~~~~~~~~~~\frac{\partial L_{tri}}{\partial \boldsymbol{x}_n} = 2(\boldsymbol{x}_a -\boldsymbol{x}_n)~~~~~~~~~~~~~~~\frac{\partial L_{ang}}{\partial \boldsymbol{x}_n} = 4\tan^2\alpha[(\boldsymbol{x}_a +\boldsymbol{x}_p) - 2\boldsymbol{x}_n]$ $~~~~~~~~~~~~~~~~~~~~~~~\frac{\partial L_{tri}}{\partial \boldsymbol{x}_p} = 2(\boldsymbol{x}_p -\boldsymbol{x}_a)~~~~~~~~~~~~~~~\frac{\partial L_{ang}}{\partial \boldsymbol{x}_p} = 2(\boldsymbol{x}_p -\boldsymbol{x}_a)-2\tan^2\alpha(\boldsymbol{x}_a +\boldsymbol{x}_p - 2\boldsymbol{x}_n)$ $~~~~~~~~~~~~~~~~~~~~~~~\frac{\partial L_{tri}}{\partial \boldsymbol{x}_a} = 2(\boldsymbol{x}_n -\boldsymbol{x}_p)~~~~~~~~~~~~~~~\frac{\partial L_{ang}}{\partial \boldsymbol{x}_a} = 2(\boldsymbol{x}_a -\boldsymbol{x}_p)-2\tan^2\alpha(\boldsymbol{x}_a +\boldsymbol{x}_p - 2\boldsymbol{x}_n)$

此外，还有各种各样的三元组样本挖掘策略，如 Hard Sample Mining (HSM) 对每个目标样本选择距离最大的同类图像和距离最小的不同类图像来构建三元组，Margin Sample Mining Loss (MSML) 结合四元组损失函数和难样本挖掘策略，以及 Correcting the Triplet Selection Bias，Smart Mining 和 Log-ratio Loss+Dense Triplet Mining 等。自适应阈值选取策略如 Hierarchical Triplet Loss 构建层次树动态计算阈值，样本生成策略如 hardness-aware deep metric learning (HDML) 由易到难生成样本来保证训练过程的高效性（这与 Curriculum Learning 的思路有点像，网络先学习简单的样本，再慢慢学习更难的样本，从而帮助网络加速收敛并找到更好的局部最优）。

基于批量数据计算的损失函数

考虑到三元组损失函数仅从一个批量中选择正负样本对，并不能充分利用批量中所有样本的信息，一些研究者提出基于批量数据计算的损失函数，包括 Liftedstruct，Histogram Loss，N-pair Loss 等。

Liftedstruct

Liftedstruct 由 Song 等人在 CVPR2016 上提出，定义如下

$$J = \frac{1}{2\hat{\mathcal{P}}} \sum \limits_{(i,j) \in \hat{\mathcal{P}}} \max(0, J_{i,j})^2$$ $$J_{i,j} = D_{i,j} + \max \left( \max \limits_{(i,k) \in \hat{\mathcal{N}}} \alpha - D_{j,k}, \max \limits_{(j,l) \in \hat{\mathcal{N}}} \alpha - D_{j,l}\right)$$ 从公式上看，该损失函数的原始形式类似 online triplet loss，只不过是针对每对正样本 $(\boldsymbol{x}_{i}, \boldsymbol{x}_{j})$ 选择双方的 hardest negative sample 来计算损失。考虑到 hinge 函数的非平滑性，该文提出优化其平滑上界

$$\tilde{J}_{i,j} = D_{i,j} + \log \left( \sum \limits_{(i,k) \in \mathcal{N}} \exp(\alpha - D_{j,k}) ＋ \sum \limits_{(j,l) \in \mathcal{N}} \exp(\alpha - D_{j,l})\right)$$

该平滑形式的损失函数则利用了每个样本的所有负样本进行损失计算。

Histogram Loss

Histogram Loss 由 Ustinova 等人在 NIPS 2016 上提出，其主要思想是最小化正样本对和负样本对的距离分布直方图之间的重叠，使得随机采样正样本对相似性小于负样本对相似性的概率越小越好。该思想有点类似于我们希望正样本之间的距离的最大值尽可能小于负样本之间的距离最小值。

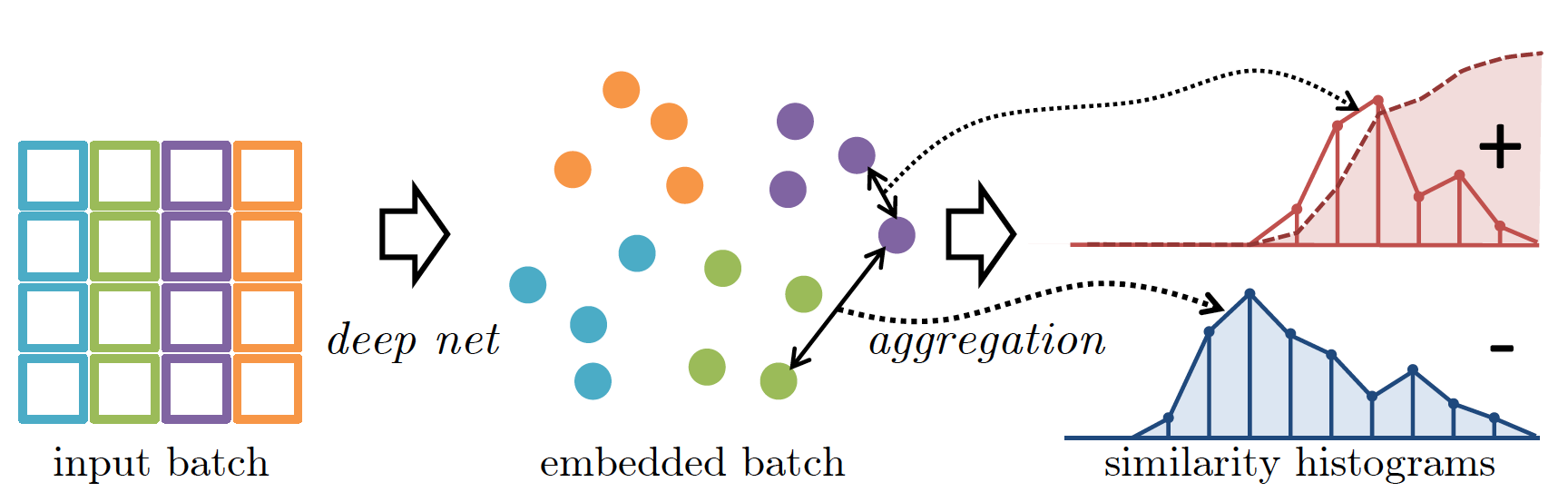
Histogram

具体来说，给定正负样本集合 $S^+$ 和 $S^-$，我们将 $[-1, +1]$ 距离划分为 $R$ 个 bin,每个 bin 的宽度为 $\Delta =\frac{2}{R-1}$，节点为 $t_1=-1, t_2, ...,t_R=+1$，距离分布直方图 $H^+$ 的每个 bin 上的值 $h_r^+$ 计算如下：

$$h_r^+ = \frac{1}{S^+} \sum \limits_{m_{i,j}=+1} \delta_{i,j,r}$$

其中

$$\begin{split} \delta_{i,j,r} = ~~~~&(s_{i,j} - t_{r-1})/\Delta~~~~~~~~~if~~s_{i,j} \in [t_{r-1}; t_r]; \\ ~~~~~~&(t_{r+1} - s_{i,j})/\Delta~~~~~~~~~if~~s_{i,j} \in [t_{r}; t_{r+1}]; \\ ~~~~~~&~~~~~~~~~~~0~~~~~~~~~~~~~~~~~~ otherwise; \end{split}$$

Histogram Loss 计算为

$$L_{hist}=\sum \limits_{r=1}^R h_r^- \left(\sum \limits_{q=1}^r h_q^+ \right)=\sum \limits_{r=1}^R h_r^- \phi_r^+$$

其中 $\phi_r^+$ 为直方图 $H^+$ 的累积和。

Histogram Loss 避免了 Triplet Loss 中的阈值和样本选择，仅需要根据 batchsize 调节 bin 的数量，在多个数据集上取得了较好的结果。此外，Histogram Loss 需要较大的 batchsize (如256) 来更准确地估计距离分布情况。

N-pair Loss

N-pair Loss 由 Kihyuk Sohn 在 NIPS 2016 上提出，其思想是针对每个目标样本区分其正样本和N－1个负样本。

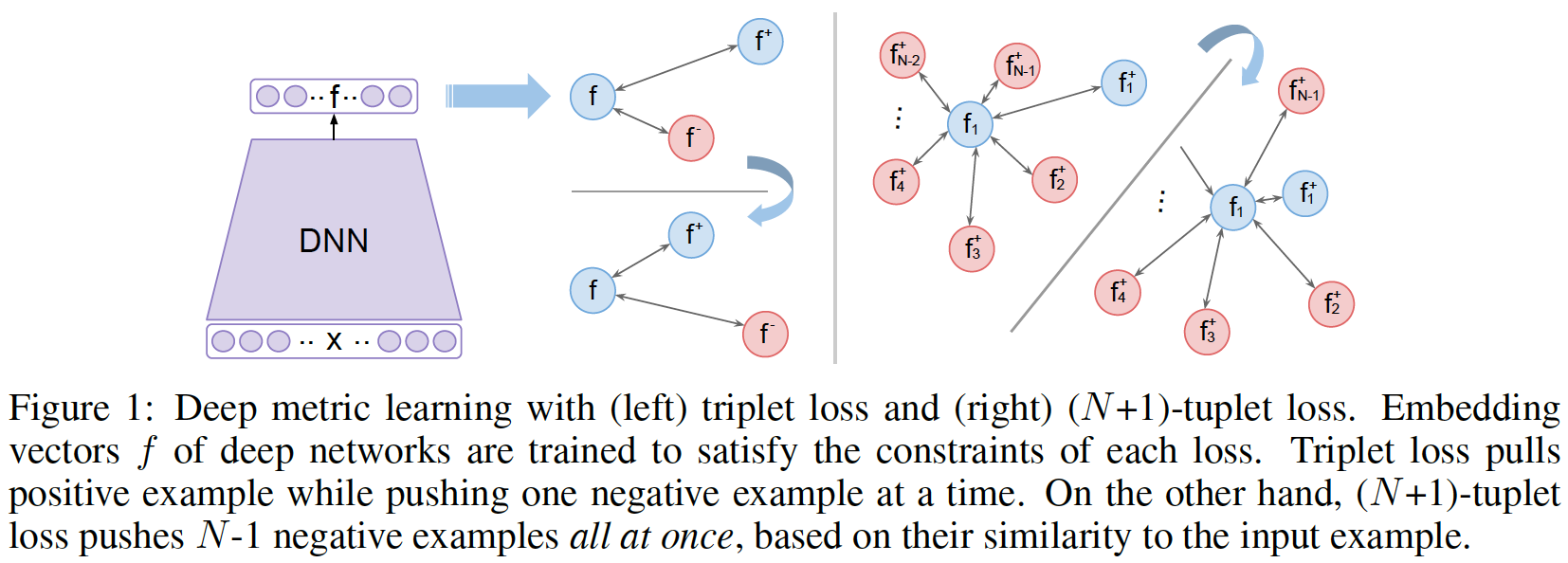
npair

N-pair Loss 定义为

$$\begin{split}L_{npair}({x, x^+, \{x_i\}_{i=1}^{N-1}}; f) &= \log(1+ \sum \limits_{i=1}^{N-1} \exp(f^{\top}f_i -f^{\top}f^+ )) \\ &= -\log \frac{\exp(f^{\top}f^+)}{\exp(f^{\top}f^+)+\sum_{i=1}^{N-1}\exp(f^{\top}f_i)}\end{split}$$

该损失函数与多分类 Softmax Loss 类似，即判断 $x$ 属于 $x^+$ 类而不属于其他负样本类。与 Triplet Loss 采用一个负样本相比，N-pair Loss 采用 $N-1$ 个负样本可以加速模型收敛。该文也提出了一种 hard negative class mining 策略，从大量不同类别中选取 C 类，随机选取1类后再逐次选择违背距离约束的其他类别。

总结

深度度量学习的目标是学习好的特征，研究的重点在于如何设计损失函数，三元组损失函数目前应用较广，但仍依赖于精巧的实现，包括计算距离时是否要对特征归一化，采用欧式距离还是余弦距离，针对不用类型的数据集如何选择正负样本对，如何选取阈值等。基于批量数据计算的度量学习能够避免三元组损失函数中繁琐的样本和阈值选择问题，但仍需要更多实际任务来验证其有效性。